Une approximation géométrique
 |
| Attention, cet article est susceptible de piquer les yeux très fort. (Animations flashouillantes et couleurs baveuses). |
Sauf que, comme vous le savez, je suis chimiste, donc je n'ai pas fait d'études supérieures me permettant de contempler la beauté derrière les objets mathématiques et de dériver toutes les propriétés de ce monde et des mondes parallèles et des mondes imaginaires à partir de mes connaissances.
Enfin, je dis ça, je suppose que c'est ce que font les mathématiciens. J'ai dû lire trop de vulgarisation.
Tout ça pour dire qu'avec huit mois de retard j'ai enfin une possible réponse à une de ces questions posées en salle des profs.
Que mon ex-collègue ne verra jamais puisque je compartimente du mieux possible le moi de la vraie vie et le moi de l'Internet.
Tant pis pour elle.
"Dis voir", tel est le préambule de la question. "Comment pourrait-on construire un polygone régulier à 16 côtés, ou un autre nombre improbable de côtés, avec du matériel basique comme une règle et un rapporteur ?"
Rappelons les termes du sujet : ce qu'elle entendait par polygone régulier (et que tout le monde entend par là, je crois), c'est une figure géométrique où tous les côtés ont la même longueur et tous les sommets sont dirigés vers l'extérieur de la figure.
Donc, ça :
Mais pas ça :
Ni ça :
En tant qu'être humain passé par une école maternelle, je n'ai aucun souci pour tracer à main levée des triangles à peu près équilatéraux et des carrés qui se tiennent.
En tant que chimiste, j'ai tracé plus que mon content de pentagones, d'hexagones, d'heptagones (merci le caprolactame) et même d'octogones.
Mais au-delà de, allez, dix sommets, je suis bien embêtée pour me sortir de là.
Avec un cercle
Une technique, si j'ai un compas, c'est de tracer un cercle et de le considérer comme le cercle circonscrit de mon polygone régulier : je sais que les 16 sommets de mon hexadécagone seront 16 points régulièrement répartis sur le cercle, je les place, je les relie, j'efface le cercle, et paf ! Polygone régulier à 16 côtés.
Pour le coup c'est assez facile de placer 16 points sur un cercle : 4 points aux quatre points cardinaux, 1 point au milieu de chacun des intervalles formés, et 1 point au milieu de chacun des nouveaux intervalles formés.
Mais si on m'avait demandé comment tracer sur papier un polygone régulier à 17 côtés, j'aurais été ennuyée.
Alors j'ai essayé une autre approche.
Avec une intuition
Vous le savez, la somme des angles de n'importe quel triangle, c'est 180°.
Vous le savez aussi, un carré ça a quatre angle de 90°, ce qui fait un total de 360° (et ce total est le même pour d'autres quadrilatères).
En m'apercevant que 360, c'est pile le double de 1802, je me suis demandé si ça se poursuivait de la même façon avec les autres polygones : si la somme des angles d'un pentagone est de 540°, si la somme des angles d'un hexagone est de 720°, etc.
En fait, si au lieu d'utiliser des degrés (°) je mesure des angles en radian, ça revient à dire que je gagne π rad dans ma somme des angles du polygone chaque fois que j'ajoute un sommet. (C'est plus facile à compter, aussi.)
Voyons voir si ça tombe juste.
 |
| Pour ceux que ça intéresserait, voilà mon fichier. |
Je vous explique :
Les colonnes "Somme °" et "Somme rad" sont les sommes des angles des polygones selon mon hypothèse. C'est peut-être un tissu de conneries.
Mais pour voir si ça colle, dans les colonnes "Angle °" et "Angle rad", j'ai calculé ce que devrait être la mesure d'un des angles du polygone si la somme des angles de mon hypothèse est la bonne. (C'est évidemment beaucoup plus lisible en degré qu'en radians).
Vérifions quelques mesures.
 |
| 107,83° mesuré VS 108° calculé |
Hey, ça passe ?
 |
| 134,72° mesuré VS 135° calculé |
Allez, c'est pas si nul comme déviation.
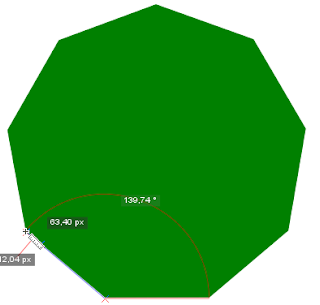 |
| 139,74° mesuré VS 140° calculé |
 |
| 144,29° mesuré VS 144° calculé |
Je devrais faire des mesures sur toutes les figures, mais comme je ne suis pas vraiment là pour prouver un truc mathématique je vais me contenter de vérifier celle sur laquelle portait la question :
 |
| 157,66° mesuré VS 157,5° calculé |
Du coup, autre méthode pour tracer un hexadécagone régulier avec seulement une règle et un rapporteur, même pas de compas :
Tu bricoles un angle de 157,5° au rapporteur3, tu poses ta règle à la longueur que tu veux, tu retraces un angle de 157,5°, tu reprends la même longueur que tout à l'heure, et tralala à force de tourner tu finis par créer ton polygone régulier à 16 côtés.
Et je ne ferai pas de gif animé récapitulatif parce que j'ai complètement la flemme.
Tout ça pour ça ?
J'espère que cette petite digression géométrique vous aura paru un peu rigolote. Les figures et les mesures sont tracées et effectuées sous Inkscape, les animations sont bricolées sous GIMP.
Une très bonne année 2017 à vous.
- J'étais horriblement nulle, mais ça vous le saviez déjà si vous avez lu cet article qui parle de mon expérience d'enseignante. Celui-là ne parlera pas de ça.
- Bac+6 les enfants, c'est ça la puissance intellectuelle.
- Et si ton rapporteur n'a pas la précision nécessaire, ma foi, c'est ton problème et pas le mien.





Bonjour @now@n,
RépondreSupprimerJe trouve ton sujet très intéressant, tu as bien exposé le problème et ta démarche pour aboutir à une solution, de façon très pédagogique. Si cela t'intéresse, ce dont tu as eu l'intuition se démontre assez bien !
Si l'on ajoute un sommet à un polygone régulier, la somme des angles du nouveau polygone régulier est augmentée de 180° (ou de pi rad).
Pour la démonstration, je prend un polygone régulier à n côtés et je trace des "rayons" partant du centre du cercle inscrit à ce polygone vers ses sommets. On a donc un ensemble de n triangles juxtaposés dans le cercle, et je note c_n les angles des triangles les plus proches du centre du cercle et a_n les angles restants, puisque les triangles sont isocèles (oui une figure aurait aidé, mais je n'arrive pas à la mettre dans mon commentaire :-) ).
L'angle c_n est simple à calculer :
c_n = 2pi/n
Cela peut se vérifier avec le triangle (2pi/3), le carré (pi/2), etc.
Puis on calcule l'angle a_n. La somme des angles d'un des triangles composants le polygone est :
2a_n + c_n = pi
2a_n = pi - 2pi/n
2a_n = (n-2)pi/n
2a_n correspond aux angles du polygone régulier du problème, tels que tu les as calculé dans ton fichier excel. La somme de ces angles est donc, puisqu'on a n triganles :
S_n = n * 2a_n
= (n-2)pi.
Si on compare la somme S_n à la somme S_n+1, c'est-à-dire la somme des angles d'un polygone régulier ayant un sommet de plus, on a :
S_n+1 - S_n = (n+1-2) - (n-2)pi
= pi !
Donc ta supposition était juste. En revanche, comme tu l'indique dans le titre de ton post, cela reste une manière approchée de tracer un polygone régulier à la règle et au compas, comme on pourrait le faire en informatique par exemple.
Je pense que ta collègue faisait référence à une méthode exacte, et celle-ci n'est pas possible pour tous les polygones réguliers. Il faut regarder du côté du théorème de Gauss-Wantzel pour avoir une condition nécessaire et
suffisant de contruction, qui fait intervenir les nombre de Fermat. https://wikimonde.com/article/Th%C3%A9or%C3%A8me_de_Gauss-Wantzel.
Il y a aussi cet article qui est un peu technique (beaucoup trop pour moi aujourd'hui ^^) http://culturemath.ens.fr/maths/pdf/geometrie/polygones.pdf, et qui propose les démonstrations. L'idée est d'arriver à construire de manière exacte un certain angle sur le cercle en y placant deux points,
de les relier et ensuite de reporter le segment sur le cercle. J'ai essayé de trouver une demonstration simple, mais je n'ai pas réussi, je me souvenais d'avoir vu cela en 1e année de prépa, mais je ne me rappelais pas
d'un truc aussi compliqué !!
Enfin, beau sujet, que l'humanité a essayé de résoudre depuis très longtemps... (voir la géométrie d'Euclide http://debart.pagesperso-orange.fr/geoplan/euclide_classique.html) et puis Gauss est passé par là.
Je suis sûr qu'il a regardé le problème en disant : "Mouaaaais... fastoche.". Pfff.
En tout cas, bonne année 2017 à toi aussi !
Alexandre